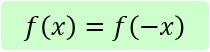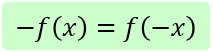Untersuchung auf Symmetrien
In der Schule kennt man zwei Arten von Symmetrien, die Achensymmetrie
und die Punktsymmetrie.
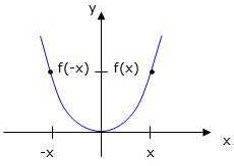
Achsensymmetrie bedeutet, dass der Graph einer Funktion an der y-Achse gespiegelt werden kann,
so dass er mit sich selbst zur Deckung kommt.
Wenn man von Punktsymmetrie spricht, meint man in der Regel die Punktsymmetrie zum Ursprung.
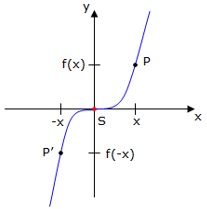
Falls der Graph einer Funktion punktsymmetrisch zum Ursprung ist, so kann man ihn am Ursprung
um 180° drehen, so dass er mit sich selbst zur Deckung kommt.
Eine Drehung um 180° ist übrigens gleichbedeutend mit einer Spiegelung
an der x-Achse, gefolgt von einer Spiegelung an der y-Achse!
Um die verschiedenen Arten von Symmetrien nachzuweisen, haben Sie in der Schule zwei
Kiterien kennen gelernt, die hier noch einmal wiederholt werden sollen.
|
Kriterium für Achsensymmetrie
|
|
Kriterium für Punktsymmetrie
|
Rechenbeispiel 1
Untersuche jeweils auf Achsensymmetrie: f(x)=x4+2x2-1 und g(x)=x3-x2.
Lösung:
f(-x)=(-x)4+2(-x)2-1=x4+2x2-1=f(x).
Somit haben wir f(-x)=f(x) nachgewiesen, d.h. f(x) ist achsensymmetrisch (zur y-Achse).
g(-x)=(-x)3-(-x)2=-x3-x2≠g(x).
Folglich ist g(x) nicht achsensymmetrisch.
Im ersten Beispiel haben wir beobachtet, dass gerade Exponenten ein mögliches Vorzeichen "zunichte" machen. Daraus gewinnen wir die folgende
Erkenntnis 1:
Ganzrationale Funktionen sind achsensymmetrisch, wenn im Funktionsterm nur gerade Potenzen vorkommen!
Rechenbeispiel 2
Untersuche jeweils auf Punktsymmetrie: f(x)=x5+x3-2x und g(x)=x3-x2.
Lösung:
f(-x)=(-x)5+(-x)3-2(-x)=-x5-x3+2x=-(x5+x3-2x)=-f(x).
Somit haben wir f(-x)=-f(x) nachgewiesen, d.h. f(x) ist punktsymmetrisch (zum Ursprung).
g(-x)=(-x)3-(-x)2=-x3-x2≠-g(x).
Folglich ist g(x) nicht achsensymmetrisch.
Im ersten Beispiel haben wir beobachtet, dass ungerade Exponenten ein Vorzeichen "erhalten". Daraus gewinnen wir die folgende
Erkenntnis 2:
Ganzrationale Funktionen sind achsensymmetrisch, wenn im Funktionsterm nur gerade Potenzen vorkommen!
Erkenntnis 3:
Kommen in einer ganzrationale Funktion genischte Exponenten vor, also sowohl gerade als auch ungerade,
so ist die Funktion weder achsensymmetrisch noch punktsymmetrisch!
Achsensymmetrie zu einer zur y-Achse parallelen Achse
Angenommen es soll nachgewiesen werden, dass eine Funktion f(x) achsensymmetrisch zur Achse x=h (nicht y=h!) ist. Wie gehen wir in einem solchen Fall vor?
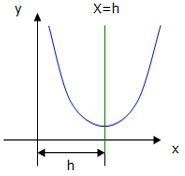
• Verschiebe f(x) um h parallel zur x-Achse und erhalte die neue Funkltion g(x)=f(x+h).
• Teste, ob für die neue Funktion g(-x)=g(x) gilt. Ist dies der Fall, so ist die ursprüngliche Funktion f(x) achsensymmetrisch zur Achse x=h.
Allgemeine Punktsymmetrie
Angenommen es soll nachgewiesen werden, dass eine Funktion f(x) punktsymmetrisch zu einem beliebigen Punkt P(a|b), also nicht unbedingt zum Ursprung, ist. Hier verfolgen wir dieselbe Idee, wie oben beschrieben.
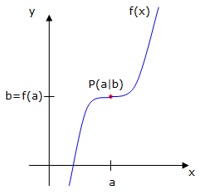
• Verschiebe f(x) in den Ursprung, also im a Einheiten nach links, wenn a positiv ist (bzw. nach rechts, wenn a negativ ist) und um b Einheiten nach unten, wenn b positiv ist (bzw. nach oben, wenn b negativ ist). Aus f(x) erhält man somit die neue Funktion g(x)=f(x+a)-b
• Teste, ob für die neue Funktion g(-x)=-g(x) gilt. Ist dies der Fall, so ist die ursprüngliche Funktion f(x) punktsymmetrisch zum Punkt P(a|b).
Rechenbeispiel 3
Untersuche f(x)=x2-4x+4 auf Achsensymmetrie zur Achse x=2.
Lösung
Verschiebe f(x) zunächst um 2 Einheiten nach links und erhalte
g(x)=f(x+2)=(x+2)2-4(x+2)+4=x2+4x+4-4x-8+4=x2.
Es gilt g(-x)=(-x)2=x2=g(x). Wir haben somit nachgewiesen, dass die verschobene Funktion g(x) achsensymmetrisch (zur y-Achse) ist.
Ergebnis: f(x) ist symmetrisch zur Achse x=2.
| Downloads |
PowerPoint